Cómo recuperar el acceso al disco duro, solucionar el error de no poder abrir el disco duro
En este artículo, te guiaremos sobre cómo recuperar el acceso a tu disco duro cuando falla. ¡Sigamos!
Fórmula para calcular el área superficial y el volumen de una esfera.
Aprendamos y repasemos la fórmula para calcular el área de superficie y el volumen de una esfera con Quantrimang.com en el artículo a continuación.
Tabla de contenido
- ¿Qué es una esfera?
- Fórmula para calcular el área superficial y el volumen de una esfera.
- Fórmula para calcular el radio de la esfera
- La esfera que circunscribe la pirámide tiene un lado perpendicular a la base.
- Tetraedro cuadrado (este es un caso especial de la fórmula 1)
- Un prisma vertical tiene una base que es un polígono inscrito.
- Fórmula para un tetraedro cuyos vértices son los vértices de un prisma recto
- Fórmula para calcular el radio de una esfera para una pirámide con caras laterales perpendiculares a la base.
- Ejemplos de cálculo de área superficial y volumen de una esfera
¿Qué es una esfera?
Una esfera es el lugar de los puntos equidistantes de un punto fijo O dado ren el espacio tridimensional. El punto O se llama centro y la distancia rse llama radio de la esfera.
¿Qué es una esfera?
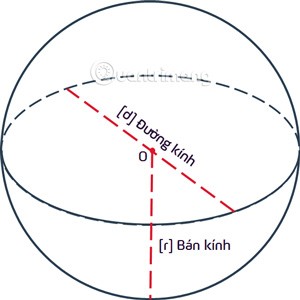
Una esfera es un conjunto de puntos que se encuentran dentro de una esfera y una esfera se llama esfera o esfera con centro O y radio r = OA.
Fórmula para calcular el área superficial y el volumen de una esfera.
Fórmula para calcular el área de la superficie de una esfera
El área de la superficie de una esfera es cuatro veces el área de un círculo grande, que es cuatro veces la constante Pi multiplicada por el cuadrado del radio de la esfera.
Fórmula para calcular el volumen de una esfera:
El volumen de una esfera, también conocido como volumen de una esfera, se calcula multiplicando tres cuartos de Pi por el cubo del radio de la esfera.
Allí dentro:
Ses el área de la superficie de la esferaVes el volumen de una esferares el radio de la esfera/esferades una esfera/esfera
Fórmula para calcular el radio de la esfera
La esfera que circunscribe la pirámide tiene un lado perpendicular a la base.
- Rd es el radio de la base.
- h es la longitud del lado perpendicular a la base.
Por ejemplo : Dada la pirámide S.ABCD con una base rectangular con AB = 3a, BC = 4a, SA = 12a y SA perpendicular a la base. Calcula el radio R de la esfera que circunscribe la pirámide S.ABCD.
Solución: Tenemos
Entonces
Tetraedro cuadrado (este es un caso especial de la fórmula 1)
El bloque cuadrado OABC tiene OA, OB, OC, perpendiculares entre sí y tiene:
Por ejemplo:
El tetraedro OABC tiene OA, OB, OC, mutuamente perpendiculares y tiene un radio de esfera circunscrito de . El mayor volumen del tetraedro OABC
Solución : Tenemos
Por otro lado tenemos:
Según la desigualdad AM – GM tenemos:
Un prisma vertical tiene una base que es un polígono inscrito.
Allí dentro:
- Rd es el radio de la base
- h es la longitud del lado.
Ejemplo 1: Dada una esfera de radio R que circunscribe un cubo de lado a. ¿Cuál de las siguientes afirmaciones es verdadera?
A.
B.
DO.
D.
Solución: Tenemos
Entonces la respuesta es C.
Fórmula para un tetraedro cuyos vértices son los vértices de un prisma recto
El tetraedro (H1) tiene vértices que son los vértices del prisma vertical (H2), luego:
Fórmula para calcular el radio de una esfera para una pirámide con caras laterales perpendiculares a la base.
En el que R, d es el radio de la base; a, x son respectivamente la longitud de la intersección de la cara lateral y la base, el ángulo en la parte superior de la cara lateral mirando hacia abajo a la base.
O puedes usar la fórmula
En el cual: Rb es el radio circunscrito de la cara lateral y a es la longitud de la intersección de la cara lateral y la base.
Por ejemplo:
Dada la pirámide S.ABCD de base cuadrada, el triángulo equilátero SAD de lado √2a y que se encuentra en un plano perpendicular a la base. Calcula el radio R de la esfera que circunscribe la pirámide S.ABCD.
A.
B.
Solución: Tenemos
Entonces la respuesta correcta es B.
Ejemplos de cálculo de área superficial y volumen de una esfera
Lección 1 : Dado un círculo con una circunferencia de 31,4 cm. Calcula el volumen de una esfera con radio igual al radio del círculo dado.
Premio:
Circunferencia del círculo C = 2πr = 31,4 cm
=> Radio r = C/2π = 5 cm
El volumen de la esfera dada es:
V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523,3 cm³
Lección 2 : Calcular el volumen de una esfera con diámetro d = 4 cm.
Premio:
Radio r = d/2 = 2 cm
El volumen de la esfera es:
V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33,49 cm³
Lección 3 :
Deje que un círculo de diámetro 4a gire alrededor de su diámetro. ¿Cuál es entonces el volumen del sólido en rotación?
Solución: Dado un círculo con diámetro 4a que gira alrededor de su diámetro, obtenemos una esfera con diámetro 4a o radio R = 2a.
El volumen de la esfera es:
Lección 4 :
La esfera con radio R√3 tiene un área de:
A. 4√3πR2
B. 4πR2
C.6πR2
D.12πR2
Solución: Aplicar la fórmula: S = 4πR2
El área superficial de una esfera con radio R√3 es: S = 4π(R√3)2 = 12πR2
Entonces la respuesta es D.
Dos fórmulas cortas pero que recordar durante mucho tiempo es bastante difícil. Marca el artículo como favorito y ábrelo cuando lo necesites. Espero que este artículo te sea útil.
Además de la fórmula para calcular el área de superficie y el volumen de una esfera anterior, también puedes consultar la fórmula para calcular el área de algunas otras formas básicas, como triángulos , rectángulos y paralelogramos. ..
Cómo usar Conversation Awareness y Live Listen en los AirPods
A primera vista, los AirPods parecen iguales a cualquier otro auricular inalámbrico. Pero todo cambió cuando se descubrieron algunas características poco conocidas.
Todo sobre iOS 26
Apple ha presentado iOS 26, una importante actualización con un nuevo diseño de vidrio esmerilado, experiencias más inteligentes y mejoras en aplicaciones conocidas.
Las mejores computadoras portátiles para estudiantes en 2025
Los estudiantes necesitan un tipo específico de portátil para sus estudios. No solo debe ser lo suficientemente potente como para desempeñarse bien en su especialidad, sino también lo suficientemente compacto y ligero como para llevarlo consigo todo el día.
Cómo agregar una impresora a Windows 10
Agregar una impresora a Windows 10 es sencillo, aunque el proceso para dispositivos con cable será diferente al de los dispositivos inalámbricos.
Cómo comprobar la RAM y detectar errores de RAM en tu ordenador con la mayor precisión
Como sabes, la RAM es un componente de hardware muy importante en una computadora, ya que actúa como memoria para procesar datos y es el factor que determina la velocidad de una laptop o PC. En el siguiente artículo, WebTech360 te presentará algunas maneras de detectar errores de RAM mediante software en Windows.
Diferencia entre un televisor normal y un Smart TV
Los televisores inteligentes realmente han conquistado el mundo. Con tantas funciones excelentes y conectividad a Internet, la tecnología ha cambiado la forma en que vemos televisión.
¿Por qué el congelador no tiene luz pero el refrigerador sí?
Los refrigeradores son electrodomésticos familiares en los hogares. Los refrigeradores suelen tener 2 compartimentos, el compartimento frío es espacioso y tiene una luz que se enciende automáticamente cada vez que el usuario lo abre, mientras que el compartimento congelador es estrecho y no tiene luz.
2 maneras de solucionar la congestión de la red que ralentiza el Wi-Fi
Las redes Wi-Fi se ven afectadas por muchos factores más allá de los enrutadores, el ancho de banda y las interferencias, pero existen algunas formas inteligentes de mejorar su red.
Cómo degradar de iOS 17 a iOS 16 sin perder datos usando Tenorshare Reiboot
Si quieres volver a iOS 16 estable en tu teléfono, aquí tienes la guía básica para desinstalar iOS 17 y pasar de iOS 17 a 16.
¿Qué le pasa al cuerpo cuando comes yogur todos los días?
El yogur es un alimento maravilloso. ¿Es bueno comer yogur todos los días? Si comes yogur todos los días, ¿cómo cambiará tu cuerpo? ¡Descubrámoslo juntos!
¿Qué tipo de arroz es mejor para la salud?
Este artículo analiza los tipos de arroz más nutritivos y cómo maximizar los beneficios para la salud del arroz que elija.
Cómo despertarse a tiempo por la mañana
Establecer un horario de sueño y una rutina para la hora de acostarse, cambiar el despertador y ajustar la dieta son algunas de las medidas que pueden ayudarle a dormir mejor y despertarse a tiempo por la mañana.
Consejos para jugar a Rent Please! Simulación de propietario para principiantes
¡Alquiler por favor! Landlord Sim es un juego de simulación para dispositivos móviles iOS y Android. Jugarás como propietario de un complejo de apartamentos y comenzarás a alquilar un apartamento con el objetivo de mejorar el interior de tus apartamentos y prepararlos para los inquilinos.
Últimos códigos de defensa de torres para baños y cómo introducirlos
Obtén el código del juego Bathroom Tower Defense de Roblox y canjéalo por emocionantes recompensas. Te ayudarán a mejorar o desbloquear torres con mayor daño.