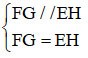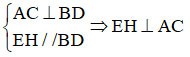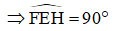Cómo calcular la diagonal de un cuadrado, cómo calcular la diagonal de un rectángulo se usa mucho en problemas de matemáticas y aplicaciones prácticas como diseño y construcción, corte de esquinas, medición... Quantrimang.com ha recopilado conocimientos sobre las propiedades de dos diagonales, así como fórmulas de cálculo, consulte para aplicar en el estudio, la vida y el trabajo.
Tabla de contenido
¿Cuál es la diagonal de un cuadrado y un rectángulo?
La diagonal de un cuadrado o rectángulo es la línea que conecta dos esquinas opuestas. Cada cuadrado y rectángulo tiene dos diagonales de igual longitud.
Cómo calcular la diagonal de un cuadrado
Propiedades de la diagonal cuadrada
- Las dos diagonales de un cuadrado tienen la misma longitud, son perpendiculares y se intersecan en el punto medio de cada una.
- Hay un círculo inscrito y un círculo circunscrito y los centros de ambos círculos coinciden y son la intersección de las dos diagonales del cuadrado.
- 1 diagonal dividirá el cuadrado en dos triángulos isósceles rectángulos.
- La intersección de las bisectrices de los ángulos, las medianas y las bisectrices perpendiculares coinciden todas en un punto.
- Tiene todas las propiedades de un rectángulo, paralelogramo y rombo.
Fórmula para calcular la diagonal de un cuadrado
Según las propiedades de un cuadrado, dos diagonales de un cuadrado son iguales y una diagonal de un cuadrado dividirá al cuadrado en dos partes de igual área, que son dos triángulos rectángulos isósceles. Por tanto, la diagonal del cuadrado es la hipotenusa de los dos triángulos rectángulos isósceles.
Entonces, para calcular la diagonal de un cuadrado, solo hay que aplicar el teorema de Pitágoras al triángulo rectángulo.
Supongamos que tienes el cuadrado ABCD con un lado de longitud a, la diagonal AC divide el cuadrado en dos triángulos rectángulos ABC y ACD.
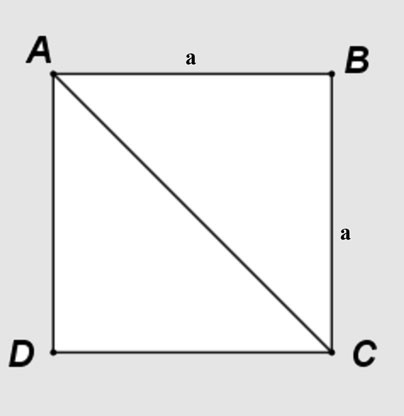
Aplicando el teorema de Pitágoras al triángulo isósceles rectángulo ABC:
⇒ ⇒
Entonces la diagonal de un cuadrado tiene una longitud de lado a:
Ejemplo de cálculo de la diagonal de un cuadrado
Ejemplo 1: Un cuadrado tiene un lado de 3cm. La diagonal de ese cuadrado es: ¿6cm, √18cm, 5cm o 4cm?
Solución:
a) Aplicando el teorema de Pitágoras en el cuadrado ABC, tenemos:
AC² = AB² + BC² = 3² + 3² = 18
=> CA = cm
Entonces la diagonal del cuadrado es √18 cm.
Ejemplo 2:
La diagonal de un cuadrado es 2dm. El lado de ese cuadrado es: ¿1cm, 3/2cm, √2cm o 4/3cm?
Premio:
Aplica el teorema de Pitágoras al triángulo rectángulo ABC, pero este ejercicio da la longitud de la diagonal, es decir AC = 2cm, calcula el lado AB.
Tenemos: AC² = AB² + BC² = 2AB (porque AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Cómo calcular la diagonal de un rectángulo
Un rectángulo es un cuadrilátero convexo con cuatro ángulos rectos, es un paralelogramo con dos diagonales iguales.
Propiedades de las diagonales de un rectángulo
Las diagonales de un rectángulo tienen varias propiedades importantes que son útiles para resolver problemas que involucran rectángulos y sus diagonales.
- La longitud de la diagonal de un rectángulo es la hipotenusa de un triángulo rectángulo, por lo que es igual a la raíz cuadrada de la suma de los cuadrados de los dos lados.
- La diagonal divide el rectángulo en dos triángulos rectángulos de igual área. Entonces, la diagonal de un rectángulo es el eje de simetría del rectángulo.
- Las dos diagonales de un rectángulo son iguales y se intersecan en el punto medio de cada línea y forman 4 triángulos isósceles.
Fórmula para calcular la diagonal de un rectángulo
A partir de las propiedades de la diagonal de un rectángulo anteriores, podemos utilizar el teorema de Pitágoras para calcular la longitud de la diagonal de un rectángulo.
Supongamos que tienes un rectángulo ABCD con longitud a y ancho b, diagonal AC como se muestra a continuación.
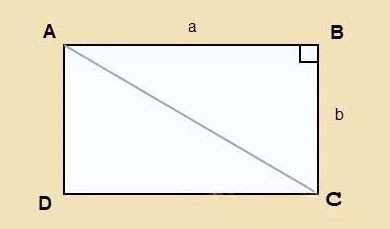
Aplicamos el teorema de Pitágoras al triángulo rectángulo ABC:
⇒ ⇒
Por lo tanto, la diagonal de un rectángulo de largo a y ancho b es:
Entonces, la longitud de la diagonal de un rectángulo es igual a la raíz cuadrada de la suma de los cuadrados de los dos lados (largo y ancho) del rectángulo.
Así, podemos calcular la diagonal de un cuadrado o rectángulo simplemente aplicando el teorema de Pitágoras.
Ejemplo de cálculo de la diagonal de un rectángulo
Calcula la longitud de la diagonal de un rectángulo con un largo de 10dm y un ancho de 5dm.
Solución:
Sea la longitud de la diagonal del rectángulo a (a > 0, dm)
Aplicando el teorema de Pitágoras, la longitud de la diagonal del rectángulo es:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Ejemplo para demostrar que un cuadrilátero es un rectángulo.
Las propiedades y la fórmula para calcular la diagonal de un rectángulo se pueden aplicar para resolver algunos problemas demostrando que un cuadrilátero es un rectángulo.
Dado el cuadrilátero ABCD tiene dos diagonales perpendiculares entre sí. Sean E, F, G, H los puntos medios de los lados AB, BC, CD, AD respectivamente. ¿Qué tipo de figura es el cuadrilátero EFGH? ¿Por qué?
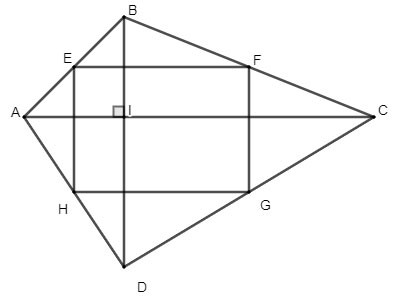
Solución:
Como E es el punto medio de AB, H es el punto medio de AD
=> EH es la mediana del triángulo ABD.
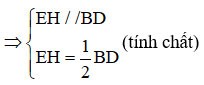 (1)
(1)
Como F es el punto medio de BC, G es el punto medio de CD
=> FG es la mediana del triángulo BCD
 (2)
(2)
De (1) y (2) =>
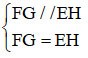
Consideremos el cuadrilátero EFGH.
FG // EH
FG = EH
=> EFGH es un paralelogramo (signo de reconocimiento)
Por otro lado:
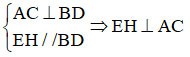
También tiene:
E es el punto medio de AB, F es el punto medio de BC.
=> EF es la mediana del triángulo ABC
=> EF // AC
Pero EH ⊥ AC => EH ⊥ EF
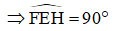
El paralelogramo EFGH tiene un ángulo recto
=> EFGH es un rectángulo



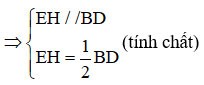 (1)
(1) (2)
(2)