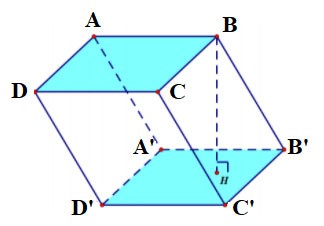
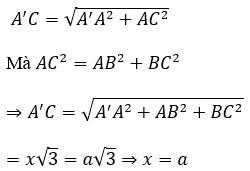Un prisma es un polígono con dos bases paralelas e iguales y caras laterales de paralelogramo.
Comentario:
- Las caras laterales de un prisma son iguales y paralelas entre sí.
- Las caras laterales son paralelogramos.
- Las dos bases de un prisma son dos polígonos iguales.
¿Cuál es la fórmula para calcular el volumen de un prisma (prisma V) y cuál es la fórmula para calcular el volumen de un prisma vertical? Consulte el artículo siguiente.
Tabla de contenido
1. Volumen de un prisma vertical
Fórmula para calcular el volumen de un prisma vertical:
El volumen de un prisma recto es igual al producto del área de la base por la altura.
Allí dentro
Ves el volumen del prisma (unidad m3)Bes el área base (unidad m2)hes la altura del prisma (unidad m)
3. Clasificación de los prismas
Prisma regular
Es un prisma vertical con base de polígono regular. Las caras laterales del prisma son todas rectángulos iguales. Por ejemplo: prisma triangular regular, cuadrilátero regular... entonces lo entendemos como prisma regular.
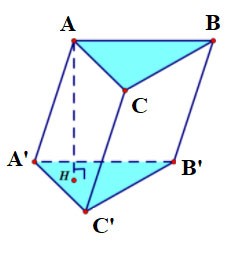
Una base cuadrilátera regular se llama prisma cuadrilátero regular.
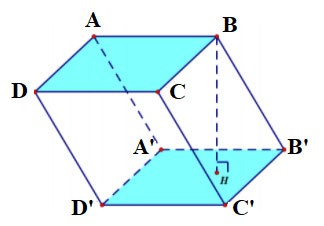
prisma triangular
- Un prisma triangular tiene 5 caras, 9 aristas y 6 vértices.
- Las dos bases son triangulares y paralelas entre sí; Cada cara lateral es un rectángulo;
- Los lados son iguales;
- La altura de un prisma triangular es la longitud de un lado.
Por ejemplo:
El prisma triangular ABC.A'B'C' tiene:
- La base inferior es el triángulo ABC, la base superior es el triángulo A'B'C';
Las caras laterales son rectángulos: AA'B'B, BB'C'C, CC'A'A;
- Bordes:
- Aristas de la base: AB, BC, CA, A'B', B'C', C'A'
- Lados: AA', BB', CC';
- Vértices: A, B, C, A', B', C'.
- La altura es la longitud de un lado: AA' o BB' o CC'.
Prisma cuadrilátero
- Un prisma cuadrilátero tiene 6 caras, 12 aristas y 8 vértices.
- Las dos bases son cuadriláteros y paralelos entre sí. Cada cara lateral es un rectángulo.
-Los lados son iguales.
- La altura de un prisma cuadrilátero es la longitud de un lado.
Por ejemplo:
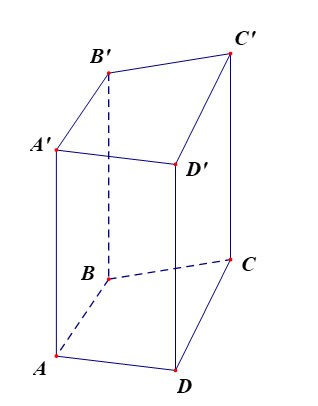
El prisma cuadrilátero ABCD.A'B'C'D' tiene:
- La base inferior es el cuadrilátero ABCD, la base superior es el cuadrilátero A'B'C'D';
Las caras laterales son rectángulos: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Bordes:
+ Aristas de la base: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Aristas laterales: AA', BB', CC', DD' son iguales.
- Vértices: A, B, C, D, A', B', C', D'.
- La altura es la longitud de un lado: AA' o BB' o CC' o DD'.
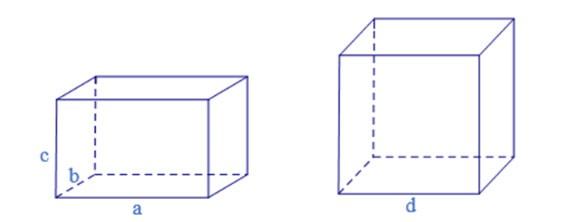
Nota: Los prismas rectangulares y los cubos también son prismas cuadriláteros.
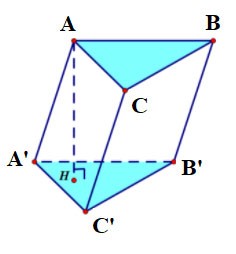
Prisma recto
Si un prisma tiene bordes laterales perpendiculares a la base, se llama prisma recto.
Nota:
Si la base es un rectángulo, el cilindro vertical del cuadrilátero se llama caja rectangular.
Si un cilindro cuadrilátero tiene 12 lados de longitud a, entonces su nombre es cubo.
Compara el prisma recto y el prisma regular:
| DEFINIR: |
NATURALEZA |
| + Un prisma vertical es un prisma con un lado perpendicular a la base. |
+ Las caras laterales de un prisma vertical son rectangulares.
+ Las caras laterales del prisma son perpendiculares a la cara base.
+ La altura es el lado
|
| + Un prisma regular es un prisma vertical cuya base es un polígono regular. |
+ Las caras laterales de un prisma son todas rectángulos iguales.
+ La altura es el lado
|
4. Ejemplo de cálculo del volumen de un prisma vertical
Ejemplo 1:
Dado el prisma ABC.A'B'C' cuya base ABC es un triángulo equilátero de lado a = 2 cm y altura h = 3 cm. Calcular el volumen de este prisma?
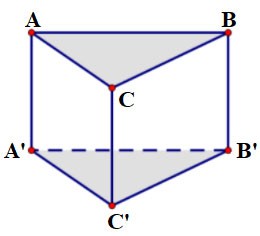
Premio:
Como la base es un triángulo equilátero con lado a, el área es:
En este momento, el volumen del prisma es:
Ejemplo 2:
Ejercicio 1: Dado un rectángulo vertical con aristas AB = 3a, AD = 2a, AA'= 2a. Calcular el volumen del bloque A'.ACD'
Instruir:
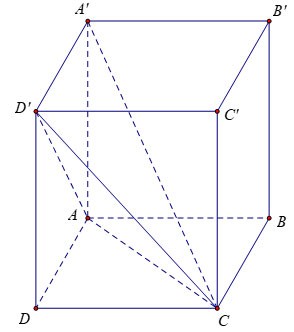
Como la cara lateral ADD'A' es un rectángulo, tenemos:
Ejemplo 3 : Dado un prisma vertical ABC.A'B'C' cuya base es un triángulo equilátero de lado a√3, el ángulo entre la base y el prisma es de 60º. Sea M el punto medio de BB'. Calcula el volumen de la pirámide M.A'B'C'.
Premio:
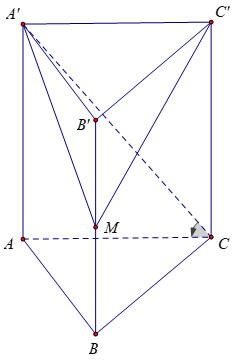
Por lo tanto, podemos inferir que
Tenemos:
Ejemplo 4:
Dado un prisma cuadrilátero regular ABCD.A'B'C'D' con una arista de base de longitud a y una cara (DBC') que forma un ángulo de 60º con la base ABCD. Calcular el volumen del prisma ABCD.A'B'C'D?
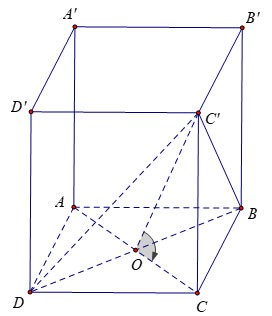
Tenemos: en el centro O del cuadrado ABCD.
Por otra parte, por tanto
Inferir
También:
Ejemplo 5:
Calcula el volumen V del cubo ABCD.A'B'C'D', sabiendo AC'=a√3
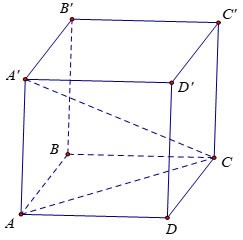
Premio:
Sea x la longitud del lado del cubo.
Consideremos el triángulo AA'C rectángulo en A con:
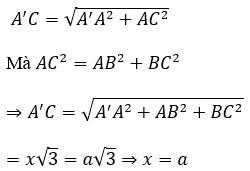
Por lo tanto, el volumen del cubo es V=a^3.
Además de la fórmula para calcular el volumen de un prisma anterior, puedes consultar más artículos sobre la fórmula para calcular el volumen de un sólido de revolución , la fórmula para calcular el área y la circunferencia de un círculo ...